개발자 끄적끄적
비연속 메모리 할당 본문
<페이징(Paging)>
- 한 프로세스의 논리 주소 공간을 동떨어진 공간들에 배정할 수 있도록 지원
- 연속 할당에서처럼 연속적인 메모리 공간을 찾거나 만들 필요 없음
- 외부 단편화 문제를 해결할 수 있는 메모리 관리 기술
- 동적 할당의 한 형태
- 모든 논리 주소는 페이징 하드웨어에 의해 물리 주소로 매핑
- 대부분의 컴퓨터 시스템에서 채택
<Frame vs. Page>
- (Page) Frame
- 물리 메모리를 고정된 크기의 블록으로 분할
- Page
- 논리 주소 공간을 하나의 frame과 같은 크기의 블록으로 분할
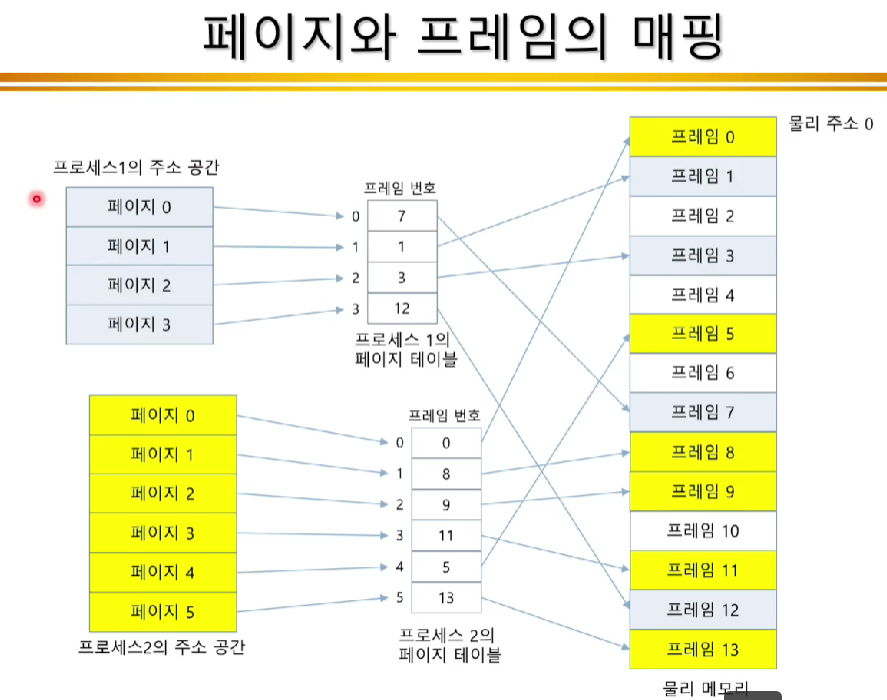
<기본 방법>
- OS는 모든 free frame들을 관리
- Frame table : 각 frame의 할당 정보 기록
- n page 크기의 프로그램 실행 위해서는 n개의 free frame을 차고, 그 곳에 적재
- 논리 주소를 물리 주소로 변환하기 위해 page table에 관련 정보 기록
- Page table
- 메모리에 각 page가 점유하는 주소를 가짐
- 자연히 사용자 프로세스는 자신에게 할당되지 않는 메모리에 접근 불가
<페이징의 특징>
- 용이한 구현
- 고정 크기로 분할하기 때문
- 높은 이식성
- 페이징을 위해 CPU에 의존하는 것 없음
- 높은 융통성
- 시스템에 따라 page 크기를 다르게 설정 가능
- 메모리 활용과 시간 오버헤드면에서 우수
- 외부 단편화는 발생하지 않음
- 내부 단편화는 발생하지만 매우 작음
- 홀 선택 알고리즘 실행 필요 없음
<페이징의 예>
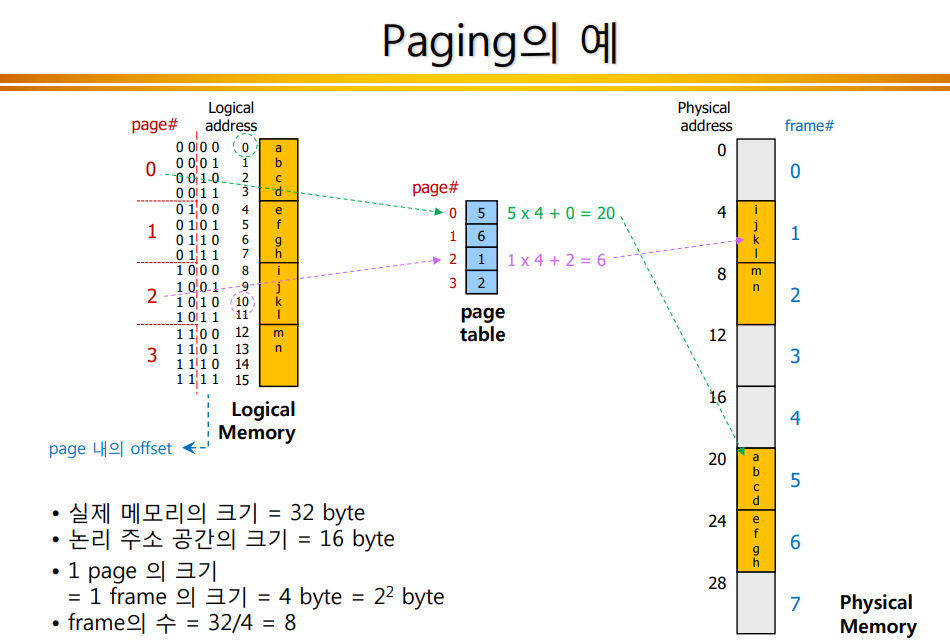
<페이지 크기(Page Size)>
- 크기는 2의 제곱으로 증가
- 보통 4Kbyte(OS에 따라 8KB, 16KB 등)
- 내부 단편화가 생길 수 있음
- 메모리는 항상 frame의 정수배로 할당되기에
- 평균적으로 프로세스 당 반(1/2) page 정도 발생
- 내부 단편화 감소 위해선 page size를 줄여야 한다
- -> page table의 크기가 커져 공간 낭비
- 디스크 입장에선 page size가 클수록 효율적
<교재에서의 내부 단편화>
- 이 단원에서는 할당외었으나 이 단원에서는 필요 없고
다음 단원을 할당 할 수 없는 영역

<32비트 CPU를 가진 컴퓨터에서 페이징 사례>
- 조건
- 4GB의 주소 공간을 갖는 프로세스
- page의 크기 4KB
- 사용자 프로세스 현황
- 총 6개 page 사용 중(프로세스 크기 = 6 x 4KB = 24KB)
- 코드 : page 0 ~ page 2에 걸쳐 있음
- 데이터 : page 2 ~ page 3에 걸쳐 있음
- 힙 : page3 ~ page 4에 걸쳐 있음
- 스택 : 사용자 공간의 맨 마지막 한 page에 할당
- page table에서 6개 항목만 사용 중
- 기본적으로 주소 공간의 모든 page를 나타낼 수 있다
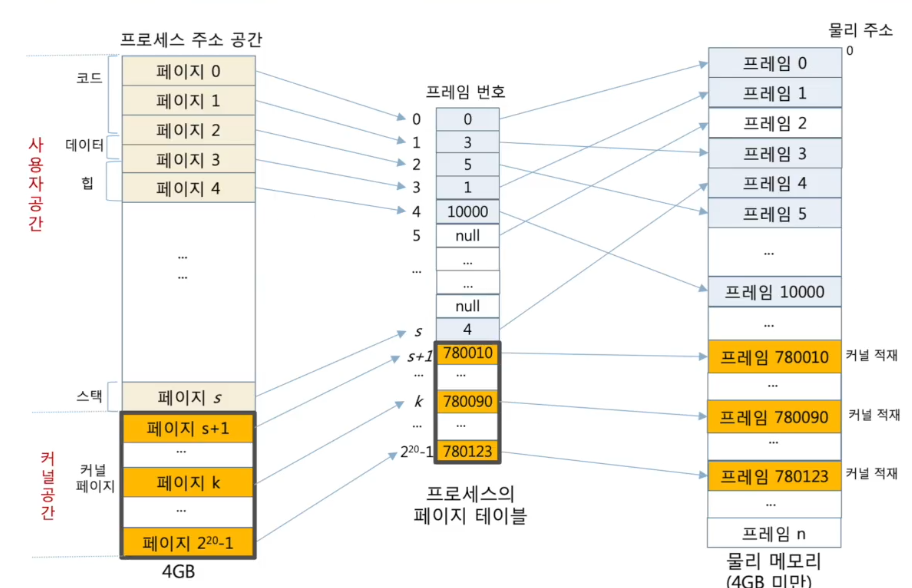
<프로세스가 동적 할당을 받는 예>
- char* p = (char*)malloc(200);
- 200 바이트만 필요하더라도 1 page(4KB) 할당
- 힙 영역의 page 5를 할당
- page 5의 논리주소 : 5 x 4KB = 20KB = 20 x 1024 = 20480
- malloc()은 page 5의 논리주소 20480을 반환
- *p = 'a';
- 논리주소 20480번지에 'a'를 저장하라는 코드
- page 5는 frame 2에 할당된다 가정
- frame 2의 물리주소 : 2 x 4KB = 8KB = 8 x 1024 = 8192
- MMU에 의해 논리주소 20480은 물리주소 8192로 매핑
- 물리 메모리 8192번지에 'a' 저장
<프로세스가 시스템 호출을 하는 예>
- 커널 공간의 page k에 담긴 커널 코드를 실행한다 가정
- 프로세스 내에서 커널 코드 역시 논리 주소로 식별
- 시스템 호출을 통해 커널 코드가 실행될 때 현재 프로세스의 page table을 이용해 물리 주소로 변환됨
- 현재 프로세스의 page table에서 page k의 frame번호 780090을 알아내고
- frame 780090에 적재된 커널 코드를 실행
<페이지와 페이지 테이블에 대한 정리(1/3)>
- page의 크기가 4KB인 32비트 CPU 가정
- 프로세스 주소 공간의 크기는?
- 1바이트(=8bit)씩 할당된 2^32개의 주소들이므로 총 4GB
- 물리 메모리의 최대 크기는?
- 물리 주소의 범위는 : 0 ~ (2^32)-1 //4GB의 미만
- 한 주소당 한 바이트 크기를 가지므로 최대 2^32바이트 = 4GB //실제 장착가능한 물리적인 메모리는 최대 4GBd이다
- 설치된 물리 메모리 크키에 비례해 프로세스의 주소 공간의 크기가 변하는가? 프로세스 주소 공간은 논리 공간(가상 공간)으로 항상 4GB
<페이지와 페이지 테이블에 대한 정리(2/3)>
- 한 프로세스는 최대 몇 개의 page로 구성되나?
- 4GB / 4KB = (2^32)/(2^12) = 2^20 = 1M개 = 약 100만개
- 각 프로세스의 page table 크기는?
- page table의 각 항목의 크기 = 32비트 = 4바이트
- 각 항목에서는 매핑되는 frame 번호를 저장해야 하므로
- 4바이트 x 2^20 = 2^22 = 4MB
- 그림 9-2에서 프로세스가 사용자 공간에서 사용하고 있는 크기는?
- 6개
<페이지와 페이지 테이블에 대한 정리(3/3)>
- page table의 모양은?
- 대부분 비어 있는 희소 테이블(sparse table) <- page는 약 100만개 중 6개만 쓰이고 있기 때문
- 낭비가 심하므로 줄이는 기법 필요
- page table은 어디에 존재하나?
- PTBR(Page Table Based Register)이 가리키는 메인 메모리에 저장
- 커널 코드도 논리 주소로 되어 있는가?
- 예 //모든 코드주소는 논리 주소로 되어있다
- CPU가 커널 코드 실행 시 물리 주소로 변환 필요
- 현재 프로세스의 page table 사용
<페이징 개념 확인(1/3)>
- 32비트 CPU, page 크기의 2KB, 물리 메모리 1GB, 프로세스 A는 사용자 공간에서 54321바이트를 차지한다 가정할 때
- 물리 메모리의 frame 크기는?
- frame의 크기는 page의 크기와 동일하므로 2KB
- frame의 개수는?
- frame은 전체 메모리를 일정한 크기로 나누어주는 것이므로
메모리 전체 크기 / 한 frame크기 = 1GB / 2KB = 2^30/2^11 = 2^19개
<페이징 개념 확인(1/3)>
- 프로세스 A가 사용중인 page의 개수는?
- 54321 / 2KB = 약 26.5 = 27개 page
- *page는 반드시 한 페이지 단위로 할당되어져야 하기 때문에 27개이다
- 프로세스 A를 적재하기 위한 물리 frame의 개수는?
- 27개의 page를 사용 중이므로 27개의 frame 할당 필요
- page table 항목의 크기가 4바이트 일 때, 프로세스 A의 page table의 크기는?
- 현재 프로세스에서 사용하고 있는 페이지 갯수와 상관없이 한 프로세스의 페이지 테이블은 현재 프로세스가 가지고 있는 모든 페이지에 대한 프레임들에 대해 매핑할 수 있어야 하므로
2^32 / 2K = 2^32 / 2^11 = 2^21개
- page table의 크기 = 2^21 x 4바이트 = 2^23바이트 = 8MB
<페이징 개념 확인(3/3)>
- 페이징에서 단편화 메모리의 평균 크기는?
- 페이징에서 외부 단편화는 일어나지 않고 내부 단편화만 일어난다
또한 페이징에서 마지막 부분만 내부 단편화가 이루어진다
즉, 코드 영역과 데이터 영역은 연속되어 있고, 마지막 page에만 내부 단편화가 발생 -> 평균 크기는 한 page의 절반이므로 2K / 2 = 1KB
- page 크기와 단편화 관계는?
- page의 크기가 크면 내부 단편화도 커질 수 잇다
- 상대적으로 영향은 미미함
- page 크기와 page table의 크기의 관계는?
- page 크기가 크면 page table 크기가 줄어든다
- page 크기의 추세는?
- 디스크 I/O 속도를 높이기 위해 커지는 추세
<Address Translation Scheme(주소변환 기법)>
- CPU에 생성된 논리 주소는 다음과 같이 나뉘어 MMU(Page table)에 의해 해석된다
- Page number : p
- Page table 접근 시 인덱스(index, ex.쪽번호)로 사용
- 각 page의 physical memory상의 base address(frame number)를 내용으로 가진다
- Page offest : d
- 특정 page 내에서의 offset(그 페이지의 시작부터 어느부분까지 떨어져있는지, ex.줄번호)으로 사용
- base address와 연결되어 physical memory address를 나타낸다
<MMU의 논리 주소 해석>
- 논리 주소 공간의 크기 : 2^m
- 한 페이지의 크기 : 2^n
- 예
- 32비트 논리 주소 체계 : 2^32
- page 크기가 4KB일 때 : 12^12


<페이징의 구현>
- 하드웨어 지원
- CPU는 PTBR(Page Table Base Register)제공
- 이 레지스터는 OS에 의해 제어된다
- MMU 장치
- page table을 참조하여 논리 주소의 물리 주소 변환
- page table을 저장/검색하는 캐시 포함
- 메모리 보호
- page 보호가 page table에 있는 지 확인
- offset이 page 범위를 넘어갔는지 확인
- OS는 page table 관리 기능 제공
- 물리 메모리에 할당된 page table과 빈 frame 리스트 생성 관리 유지
- 프로세스 생성/소멸에 따라 동적으로 frame 할당 및 반환 처리
- page table 갱신
- 컨텍스트 스위칭 시 PTBR 로딩
<페이지 테이블 사용시 문제점>
- 한 번의 메모리 조작을 위해 두 번의 메모리 접근 발생
- 각 page table은 수 MB 크기로 메모리 저장됨
- CPU가 메모리 접근시마다 2번의 메모리 접근 필요
- 실행 속도 저하
- -> TLB 사용으로 해결
- page table의 낭비
- 프로세스의 실제 크기는 매우 작아 대부분의 page table 항목이 비어있다
- 프로세스의 최대 크기 기준으로 page table을 형성했기에
- -> 2-레벨 page table 등의 방법 제안
<Page table 속도 저하 문제 해결 방법>
- Translation Look-aside Buffers : TLBs
- 특수한 고속의 하드웨어 캐쉬를 이용해 메모리 접근 문제를 해결
- 주소 변환 개시로 불림
- 최근에 접근한 page 번호와 frame 번호 쌍을 항목으로 저장
- 현대 컴퓨터에서는 MMU 내에 존재
- 연관메모리(Associative memory)
- key + value
- 병렬 검색으로 빠른 검색 가능하지만 비용이 많이 드는 하드웨어
<연관 메모리(Associativie Memory)>
- 동시에 여러 key(page number)와 비교
- page 번호 발견 시(TLB hit)
- 그에 대응하는 frame 번호 알려줌
- page 번호 미발견시(TLB miss)
- 메모리에 있는 page table에서 찾아 TLB에 추가
- 교체 작업 필요
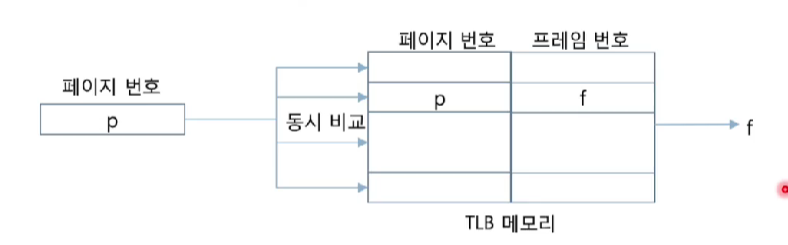
<TLB와 참조의 지역성>
- TLB는 참조의 지역성으로 인해 효과적인 전략임
- TLB 사용 시 순차 접근 시 실행 속도 빠름
- TLB 사용 시 임의 접근이나 반복이 없는 경우엔 느림
- TLB miss로 TLB 항목 잦은 교체 발생
<TLB 성능>
- TLB 히트율을 높이기 위해선 TLB 항목수 늘리기
- 비용과 상충
- page가 클수록
- TLB 히트 증가 -> 실행 성능 향상
- 내부 단편화 증가 -> 메모리 낭비
- TLB 도달 범위(TLB reach)
- TLB의 모든 항목에 채워졌을 때 miss 없이 접근할 수 있는 메모리 접근 범위
- TLB 항목수 x page 크기
<TLB가 있는 경우의 실행 과정>
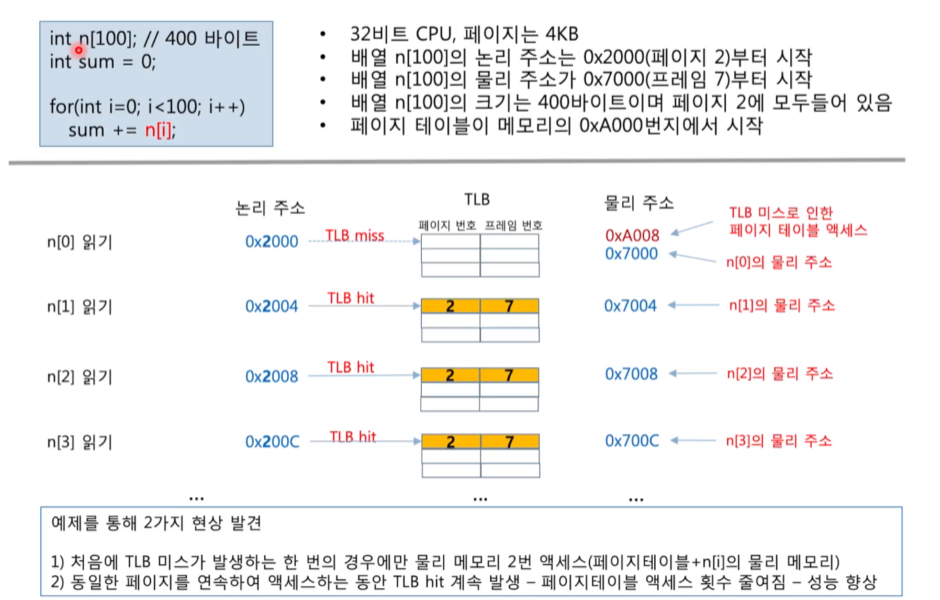
<TLB를 가진 경우에 메모리 액세스 과정>
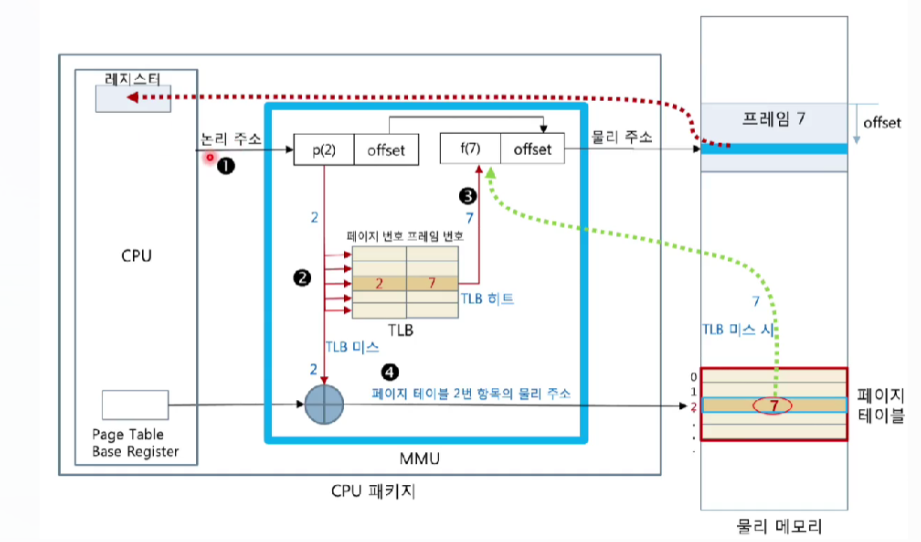
<TLB를 고려한 컨텍스트 전환 과정>
1. CPU의 모든 레지스터를 PCB에 저장
2. 새로 스케줄된 프로세스의 PCB에 저장된 page table의 주소를 CPU의 PTBR에 적재
3. TLB 캐시의 모든 항목을 지움
- 이전 프로세스 잔재이므로
4. 새 프로세스의 PCB에 저장된 레지스터 값들을 CPU에 적재 후 실행 재개
- 이후 TLB miss가 발생하며 TLB 항목이 채워져 감
<2개의 페이지에 걸쳐있는 배열>
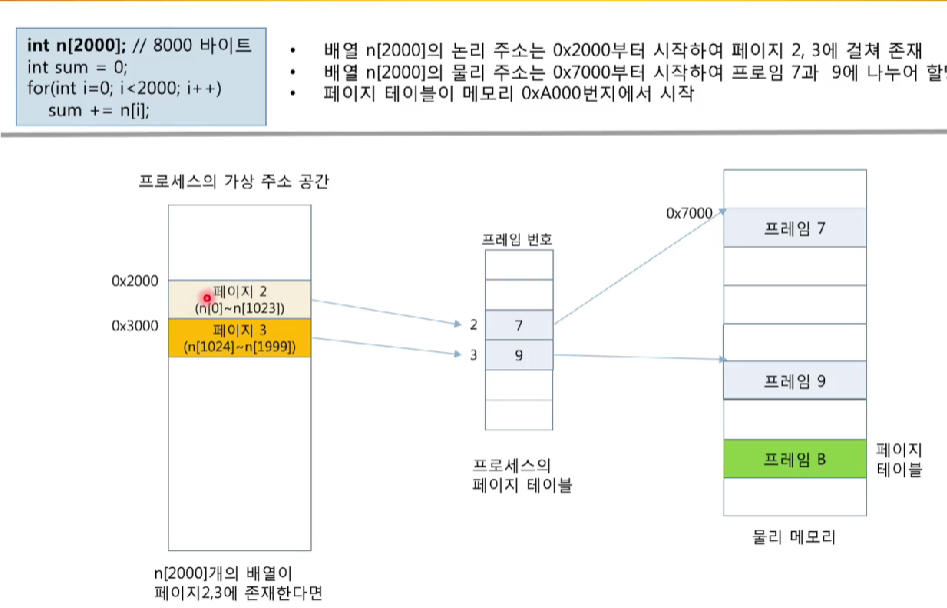
<페이지 테이블의 메모리 낭비>
- 32비트 CPU에서 프로세스당 page table 크기
- 프로세스의 주소 공간 : 4GB(프로세스의 논리주소공간)/4KB(각 페이지의 크기) = 2^32/3^12 = 2^20 = 1M개의 page로 구성
- 프로세스당 page table의 크기
- 한 항목이 4바이트이면 2^20개 x 4바이트 = 4MB
- 10MB 메모리를 사용하는 프로세스 가정 시
- 실제 활용되는 page table 항목 수
- 10MB / 4KB = 10 x 2^20 / 2^12 = 10 x 2^8 = 2560개
- 실제 활용되는 page table 비율
- 10 x 2^8 / 2^20 = 10/2^12 = 약 0.0024
- 매우 낮음
<페이지 테이블 낭비 문제의 해결책>
- 역 페이지 테이블
- 멀티 레벨 페이지 테이블
<역 페이지 테이블(Inverted Page Table, IPT)>
- Page table을 물리 주소 공간에 대응시켜 구성
- 일반적으로는 프로세스마다 논리 주소 공간에 대응
- 각 항목은 메모리의 frame에 대응
- 시스템 전체에 단 하나의 page table만 존재
- 역 페이지 테이블 항목의 수 = frame의 수
- 구성
- 역 페이지 테이블의 인덱스 = frame 번호
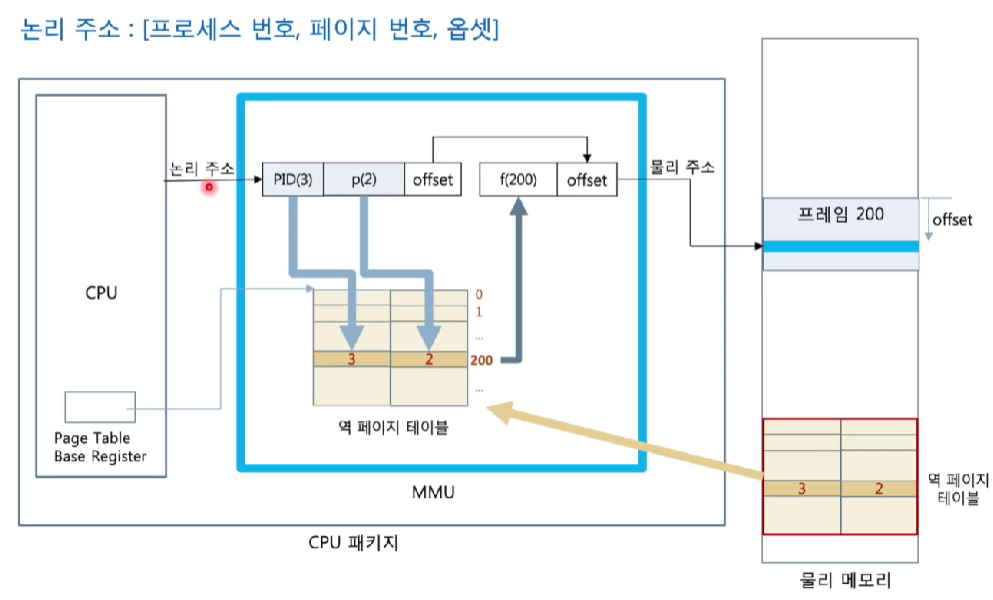
- 역 페이지 테이블 항목 = [pid, p]
- 논리 주소 형식 = [pid, p, offset]
<역페이지 테이블의 예>
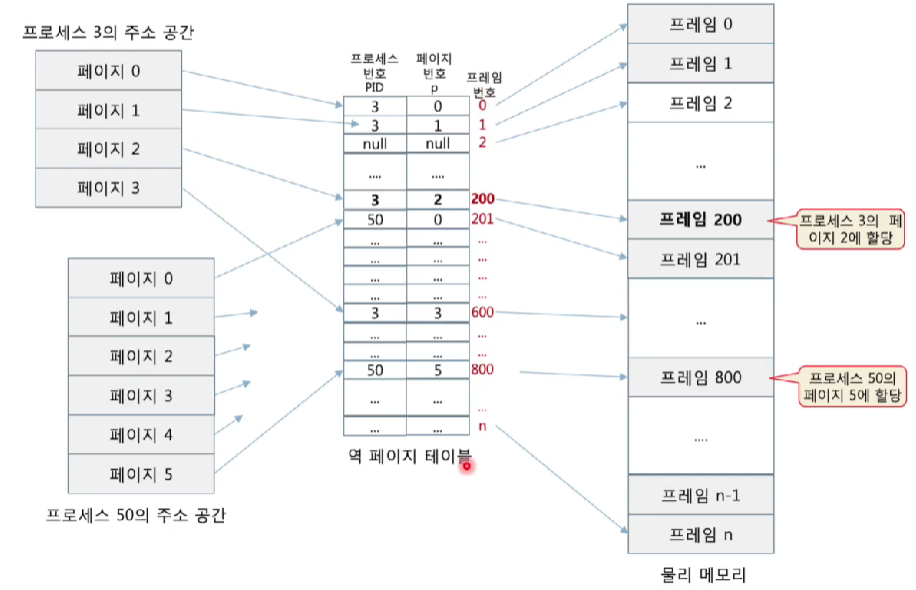
<역페이지 테이블을 이용한 매핑>
<역 페이지 테이블의 크기>
- 역 페이지 테이블의 항목 크기
- 프로세스 번호(pid)와 page 번호(p)로 구성
- pid와 p가 각각 4바이트라면 항목 크기는 8바이트
- 역 페이지 테이블의 항목 수
= 물리 메모리 크기 / 프레임 크기
- 물리 메모리가 4GB, 프레임 크기 4KB이면
- 역 페이지 테이블 항목 수 = 4GB/4KB = 2^20개 = 약 100만개
- 역 페이지 테이블의 크기 = 2^20개 x 8바이트 = 8MB
- 10개의 프로세스가 실행 중일 때
- 기존의 page table의 크기 = 10 x 4MB = 40MB
- 역 페이지 테이블의 크기 = 8MB
- 시스템에 1개만 존재
<역 페이지 테이블의 특징>
- Page table 크기를 획기적으로 줄일 수 있음
- 특정 page frame을 탐색하기 위해 더 많은 시간 소요
- Page table 전체를 검색해야 하기에
- 탐색시간을 줄이기 위해 hash table 사용
- -> 3번의 메모리 조작 발생
- hash table -> inverted page table -> 주기억장치
- 연관 메모리(Associate memory)사용
- 고가의 비용
<멀티 레벨 페이지 테이블(multi-level page table)>
- 논리주소 공간을 여러 단계의 page table로 나눔
- 대용량의 page table을 주기억장치처럼 취급하여 다시 페이징 함
- Page table 자체를 위한 paging 기법
- 사용중인 page들에 대해서만 page table 구성
- 기존 page table의 낭비를 줄임
- 간단한 예 :
- 2-레벨 페이징 기법(Two-level paging scheme)
- Page table을 다시 페이징 함
<2-레벨 페이지 테이블>
- page table을 다시 페이징
- 논리 주소의 page 번호 부분을 2개의 레벨로 나눔
page number(20비트) | offset(12비트)
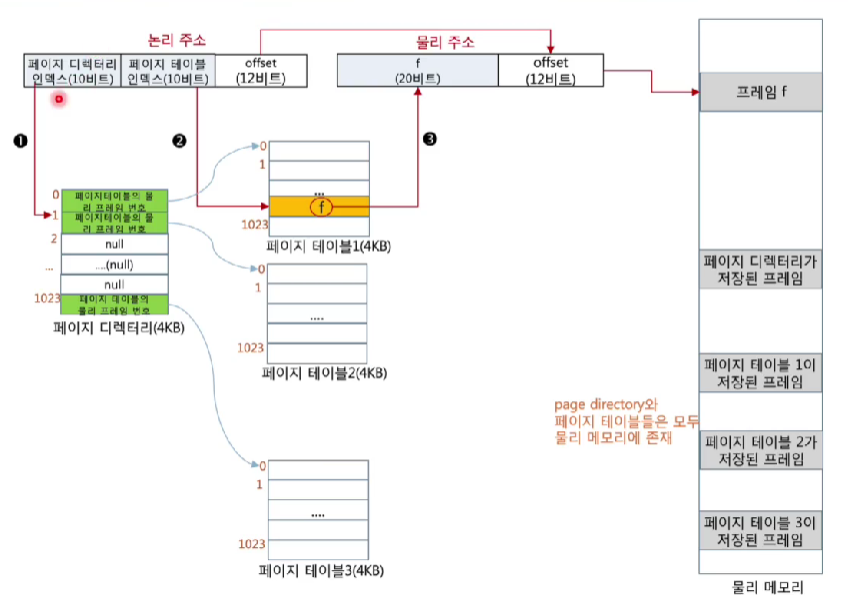
page directory index(10비트) | page table index(10비트) | offset(12비트)
- 논리 주소 구성
- [페이지 디렉터리 인덱스, 페이지 테이블 인덱스, 옵셋(offset)]
- page 크기 4KB 일 때
- 논리 주소의 하위 12비트 : page 내 옵셋 주소
- 논리 주소의 상위 20비트 : page 디렉터리 인덱스와 page 테이블 인덱스
<2-레벨 페이지의 사례>
<세그멘테이션(Segmentation)>
- 가변길이의 연관된 정보들의 집합
- 각 segment들은 '이름'과 '길이'를 가짐
- 외부 단편화 발생
- 내부 단편화는 없음
- 사용자 관점에서의 메모리 관리 기법
- 논리 주소 공간을 segment들의 집합으로 정의
- 코드, 데이터, 스택, 힙 세그먼트
- 프로세스를 segment로 나누는 과정은 컴파일러, 링커, 로더, OS에 의해 이루어진다
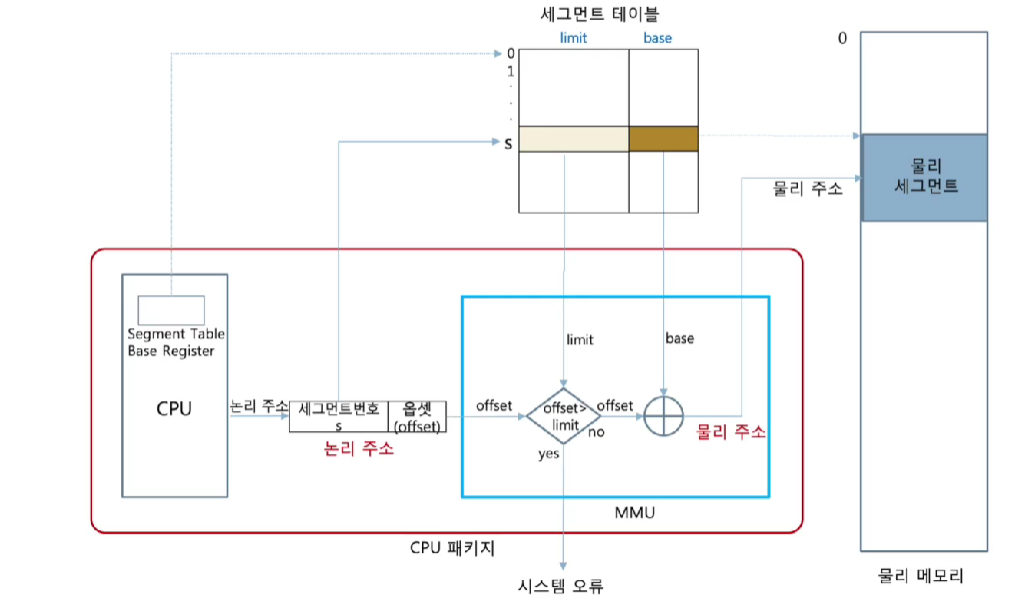
<세그멘테이션 주소 매핑>
<세그멘테이션의 구현(1/2)>
- 논리 주소 구성
segment number(s) | segment offset(d)
- 하드웨어 지원
- CPU STBR(Segment Table Base Register)
- segment table에 대한 메모리상의 시작 주소
- MMU
- 논리 주소를 물리 주소로 매핑
- 논리 주소가 segment 범위를 넘어서는지 판별
- segment table
- 각 segment 별로 시작 주소와 길이 정보 유지
<세그멘테이션의 구현(2/2)>
- 운영체제의 지원
- segment의 동적 할당/반환 및 segment table 관리 기능 구현
- 프로세스 생성/소멸에 따라 동적으로 할당/반환
- 물리 메모리에 할당된 segment table과 자유 공간에 대한 자료 유지
- 컨텍스트 스위칭 때 CPU 레지스터에 적절한 값 적재
- 컴파일러, 링커, 로더의 지원
- 프로그램을 세그먼트 기반으로 컴파일 링킹, 로딩
<예 : The Intel Pentium>
- 2가지 구조를 동시에 지원
- Pure segmentation
- Segmentation with paging
- Segment를 paging 함
- ex) 'CPU' -> logical address -> 'Segmentation Unit' -> linear address -> 'Paging Unit' -> physical address -> 'Physical Memory(물리적 메모리)'

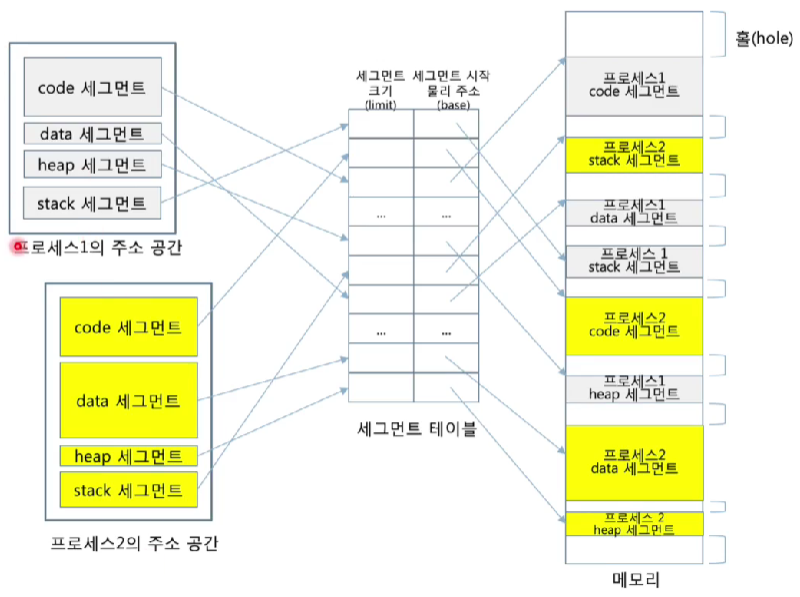
<논리 세그먼트와 물리 세그먼트 매핑>
'운영체제' 카테고리의 다른 글
| 가상메모리(1) (0) | 2024.05.22 |
|---|---|
| 메모리 관리 (0) | 2024.05.10 |
| 식사하는 철학자 문제 (1) | 2024.05.01 |



